Google Questions And Answers API

{
  ...
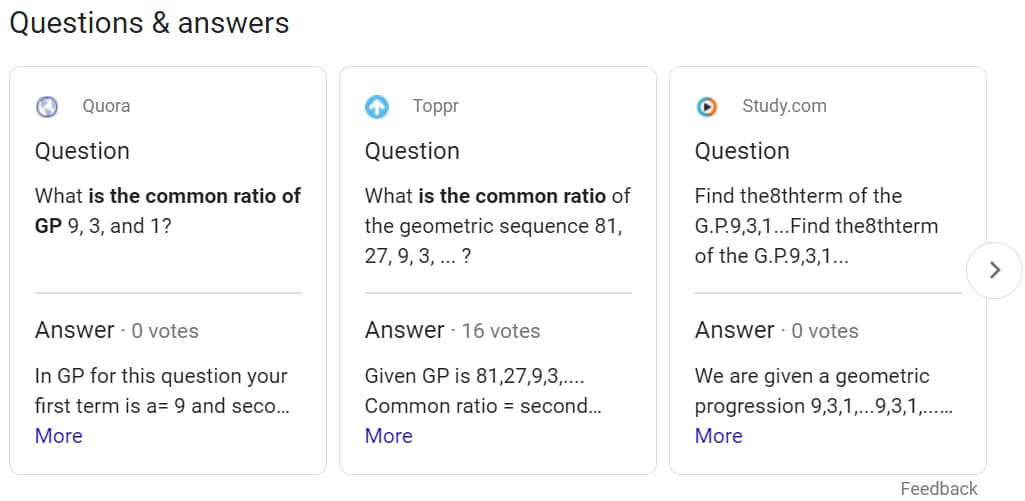
  "questions_and_answers": [
    {
      "link": "https://www.quora.com/What-is-the-common-ratio-of-GP-9-3-and-1",
      "source": "Quora",
      "question": "What is the common ratio of GP 9, 3, and 1?",
      "answer": "In GP for this question your first term is a= 9 and second term is at= 3 and third term is ar^2 to find the ratio second term is divided by first term and third term is divided by second term and so on 3/9= 1/3 1/3=1/3 therefore its common ratio is 1/3",
      "votes": 0
    },
    {
      "link": "https://www.toppr.com/ask/question/what-is-the-common-ratio-of-the-geometric-sequence-81-27-9-3/",
      "source": "Toppr",
      "question": "What is the common ratio of the geometric sequence 81, 27, 9, 3, ... ?",
      "answer": "Given GP is 81,27,9,3,.... Common ratio = second numberfirst number = 2781 = 13 So, the common ratio is 13 .",
      "votes": 16
    },
    {
      "link": "https://study.com/academy/answer/find-the-8th-term-of-the-g-p-9-3-1.html",
      "source": "Study.com",
      "question": "Find the8thterm of the G.P.9,3,1...Find the8thterm of the G.P.9,3,1...",
      "answer": "We are given a geometric progression 9,3,1,...9,3,1,... and we are asked to find the 8th term. We can find the nth term in a geometric progression if we use the formula written below. an=a1rn−1an=a1rn−1 The term a1a1 here represents the first term of the sequence and rr is the common ratio. For this particular sequence, we know that the first term is a1=9a1=9. As for the common ratio, we can simply solve it by dividing the second term by the first term. r=a2a1=39=13r=a2a1=39=13 We can now solve for the 8th term by substituting n=8n=8 and the other required values in the formula. a8=9(13)8−1=9(12187)=92187=1243a8=9(13)8−1=9(12187)=92187=1243 Therefore, the 8th term of the sequence is 12431243.",
      "votes": 0
    },
    ...
  ],
  ...
}